A perfect strategy for roulette?

This case study uses SCOOP to model a strategy for the roulette casino game. Combining forces with CADP and MRMC, we compute the probability of going home with a profit.

The game

The game of roulette goes as follows: the dealer spins a little ball, which lands on a number between 0 and 36 according to a uniform distribution. Hence, the probability of each outcome is 1/37. The player can bet on several items, two of which are the guess that the outcome is either even or odd. He wins if the actual outcome corresponds to his guess (except for the outcome 0, in which case nobody wins).

We explore a strategy that seems to maximise our probability of winning. Basically, we just always guess on even and double the stakes each time we loose. Initially we bet 1 euro. If we win, we go home with a profit. If we loose, we bet 2 euros. Again, if we win we go home, otherwise we bet 4 euros. It is easy to see that, no matter how many times we loose, at some point we will win and then receive precisely the amount of money we lost so far increased by 1 euro. Hence, we will always go home 1 euro richer.

Unfortunately, in practice this strategy will not always work. After all, the amount of money we bet increases exponentially with the number of losses, so we will quickly be out of money and therefore not able to continu the strategy. Additionally, several casino's have put a limit on the amount of money that can be bet in one round.

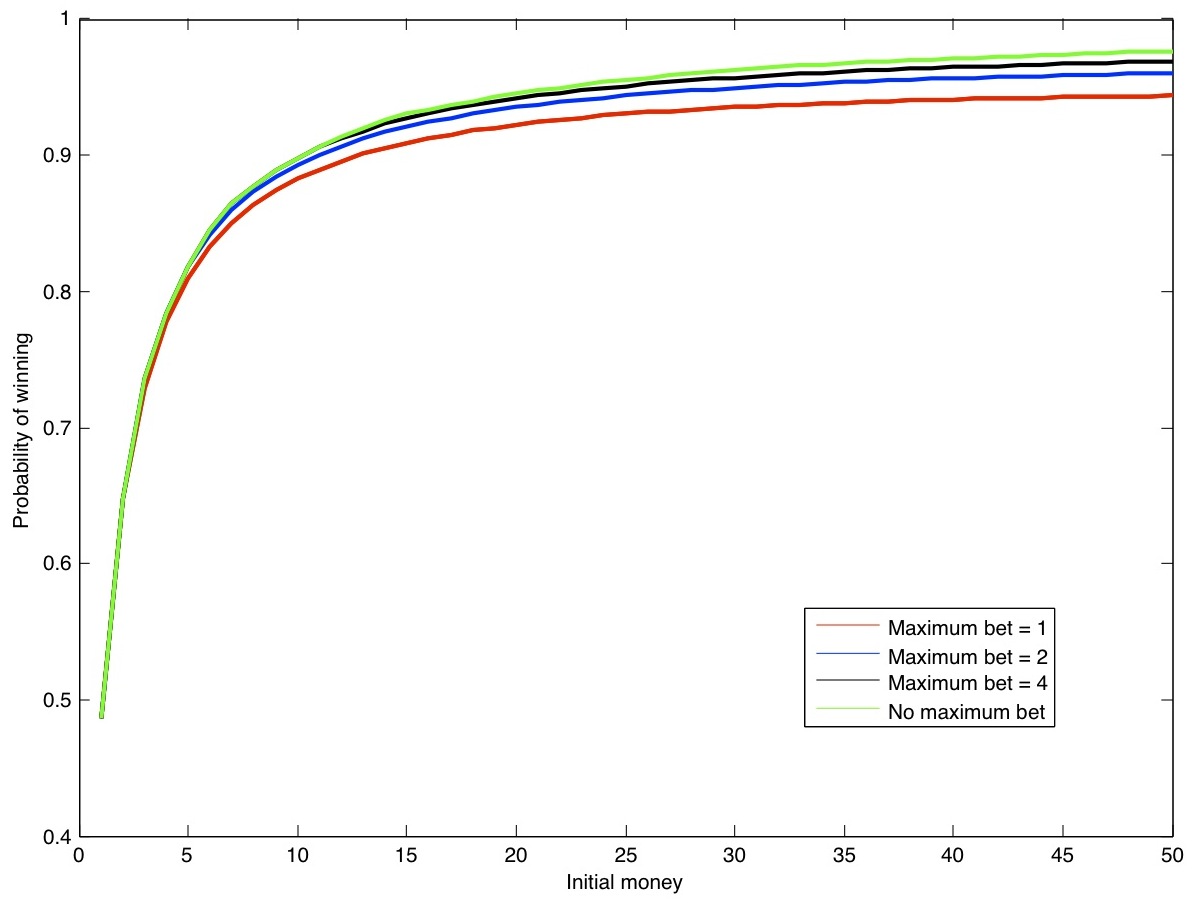
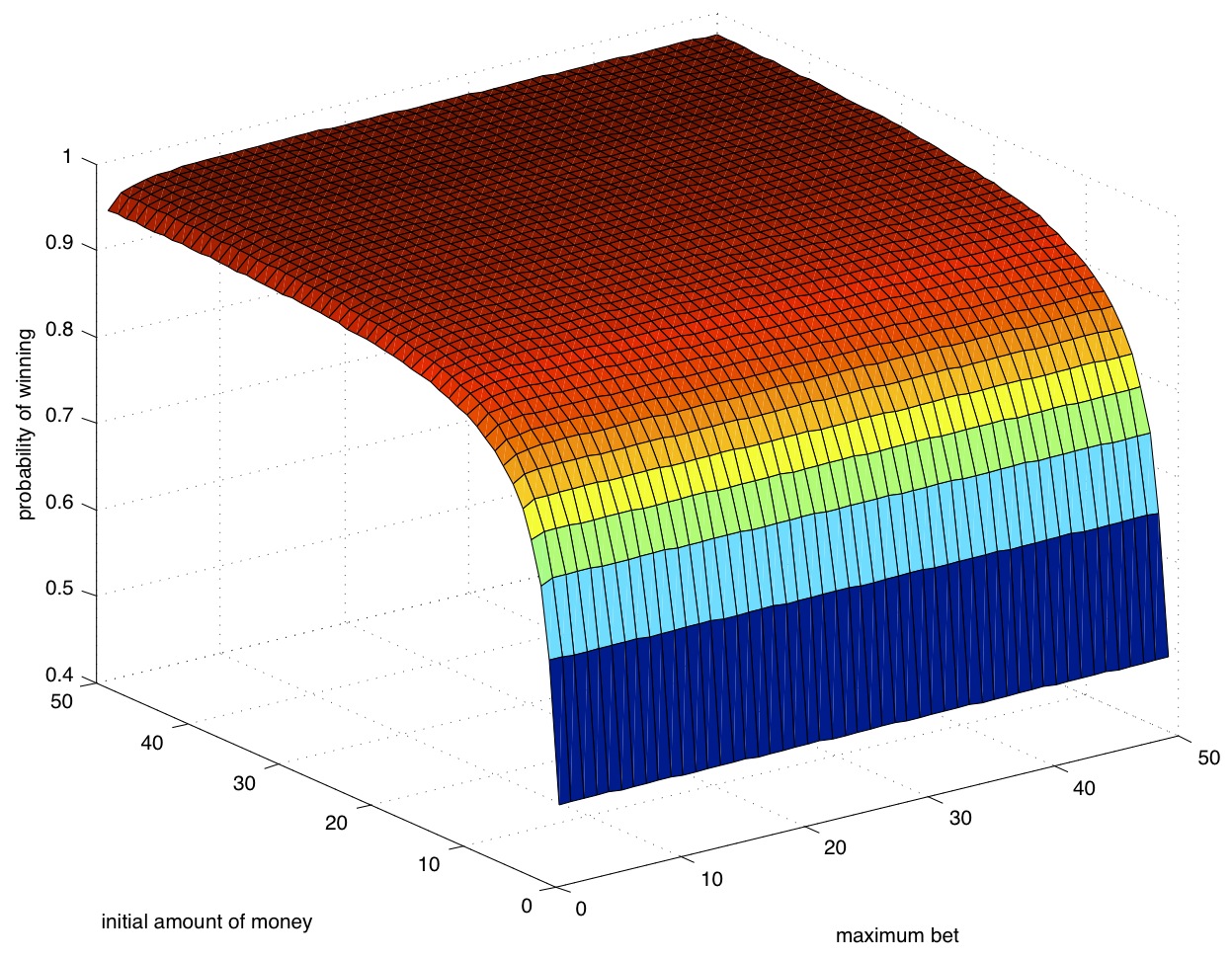
Based on the observations above, we investigate the winning probabilities of this strategy for different initial amount of money and different betting limits.

The SCOOP model

It is not so difficult to model this game, including the strategy, in SCOOP.

For ease of modelling, we introduce four types:
type Bet = {1..2*maximumBet} type Money = {0..initialMoney+1} type Outcome = {0..36} type Guess = (even, odd)
The types are based on two constants, which will be instantiated during the state space generation: maximumBet and initialMoney. Note that the amount of money we have never exceeds the initial amount increased by 1, since the strategy forces us to go home after reaching precisely this point. At some point the bet may be more than the maximum bet, but this will be resolved later on.

Based on these types, we can model some processes. First, we model the player:
SmartPlayer(m:Money, nextBet:Bet) = m = 0 | m > initialMoney => Finished[m] ++ m > 0 & m <= initialMoney => Play[m,min(m, min(nextBet, maximumBet))]
A player is characterised by the amount of money he has, and by the amount of money he will bet in the next round. If he doesn't have any money left or made a profit, he quits. Otherwise, he will bet again, following our strategy. Note that it is only possible to follow the strategy if we have enough money and if the betting limit does not prohibit us from betting the required amount. Therefore, we take a minimum over the amount of money we have, the limit and the bet according to the strategy.

In case the game in finished, we output the result:
Finished(m:Money) = m = 0 => broke . Finished[m] ++ m > 0 => quit(m) . Finished[m]
In case we play, we guess even, the dealer spins the ball and we obtain an outcome. Instead of giving each outcome a probability of 1/37, we chose to give 1 and 2 both a probability of 18/37, to give 0 a probability of 1/37 and to give a probability of 0 to all other outcomes. Clearly, this is equivalent to the actual situation, it doesn't matter which specific number we get, only whether it is odd, even, or 0.
Play(m:Money, b:Bet) = guess(even). deal. psum(o:Outcome, ifthenelse(o=1, 18/37, ifthenelse(o=2, 18/37, ifthenelse(o=0, 1/37, 0))): outcome(o) . (o = 0 => loose.SmartPlayer[m-b,b*2] ++ o > 0 => Decision[even,o,m,b]))
If the outcome is 0, we lost. In that case, we continu after subtracting the bet from our amount of money and doubling the bet. Otherwise, we use the process Decision to decide on the outcome of the bet. It checks whether the parity of the outcome corresponds to the guess. If not, we continu as above. If so, the bet is added to our amount of money and in the bet for the next round is set to 1. (Note that winning one round does not immediately implies that we made a profit and will quit; after all,it could be the case that our bet was lower than what is prescribed by the strategy, due to us running out of cash or not being allowed to exceed the table limit.)
Decision(g:Guess, o:Outcome, m:Money, b:Bet) = g = even => (mod(o,2) = 0 => win.SmartPlayer[m+b,1] ++ mod(o,2) = 1 => loose.SmartPlayer[m-b,2*b]) ++ g = odd => (mod(o,2) = 1 => win.SmartPlayer[m+b,1] ++ mod(o,2) = 0 => loose.SmartPlayer[m-b,2*b])
Finally, the model has to be initiated and some actions can be hidden.
init SmartPlayer[initialMoney,1] hide guess, deal, win, outcome, loose
The complete model is incorporated in the web-based version of SCOOP, and can also be found here.

Analysing the model

It is easy to let SCOOP generate a state space of this model, but in the end we are interested in the probability of going home with a profit. For this, we will use the model checker MRMC. Since SCOOP only uses heurstics for reducing the model size, clearly in general it does not generate the minimal probabilistic automaton. Therefore, it turns out that we can best first minimise the state space modulo probabilistic branching bisimulation, before feeding it to MRMC. For this minimisation step, the BCG_MIN tool of the CADP toolset is perfectly applicable.

The steps we take to minimise the state space are as follows: Next, we want to compute the probability of going broke. For this purpose, we want to obtain a DTMC model to analyse with MRMC. Note that this is indeed possible, since we constructed the model such that there is no nondeterminism left.

To simplify things, we created a small Java program that takes an AUT file and produces the corresponding TRA and LAB files that are asked for by MRMC. It can be downloaded here and applied as follows: Note that DTMCs do not have labelled transitions, only probabilistic transitions. Moreover, state labels are used for model checking purposes. Since we are interested in the probability of reaching the self-loop broke of the finished process, the Java program just transfers all non-labelled transitions to the DMTC and changes all labelled transitions to state labels. Since we are not interested in the behaviour after reaching these states, no harm is done.

Finally, we can apply MRMC to compute the probability of going broke. We need the following commands:
P {>= 0 } [tt U broke] $RESULT[1]
A file that contains these (plus some additional commands to switch off debug information) can be found here. It can be applied as follows: On the bottom, we find $RESULT[1] = 0.0161264. Apparently, when starting with 100 euros and having a betting limit of 10, the probabilty of going home broke is 0.016, and the probability of going home with 101 euro is 1-0.016 = 0.984. Note that, clearly, this still yields an expected value below our initial amount: 101 x 0.984 + 1 x 0.016 = 99.4 euro.

Experimenting with several instances of the model

We are interested in finding out the probability of winning for a variety of values for initialMoney and maximumBet. Therefore, we used this script to perform the above steps for all combinations (i,j) for these variables for 1 <= i,j <= 50. The script uses an additional little program to parse the output of MRMC. It can be compiled using The script only reduces via CADP if the initial amount is more than 40 euros, since it turned out that no speedup is obtained before that. Also, if j > i, then the value for (i,j) is shown, since a maximum bet larger than the initial amount is clearly never needed due to our strategy. This way, we generated the graphs below. You can click on them to obtain larger versions.